二分图匹配

设$G=(V,E)$（$V$为点集，$E$为边集）是一个无向图，如果顶点$V$可分割为两个互不相交的子集$(A,B)$，并且图中的每条边$(i，j)$所关联的两个顶点$i$和$j$分别属于这两个不同的顶点集 $(i \in A,j \in B)$，则称图$G$为一个二分图……

一 定义

1 什么是二分图

• 设$G=(V,E)$（$V$为点集，$E$为边集）是一个无向图，如果顶点$V$可分割为两个互不相交的子集$(A,B)$，并且图中的每条边$(i，j)$所关联的两个顶点$i$和$j$分别属于这两个不同的顶点集 $(i \in A,j \in B)$，则称图$G$为一个二分图。

如下图，一张图被分为$U$，$V$两个点集，每个点集内部均无边，则是一个二分图。

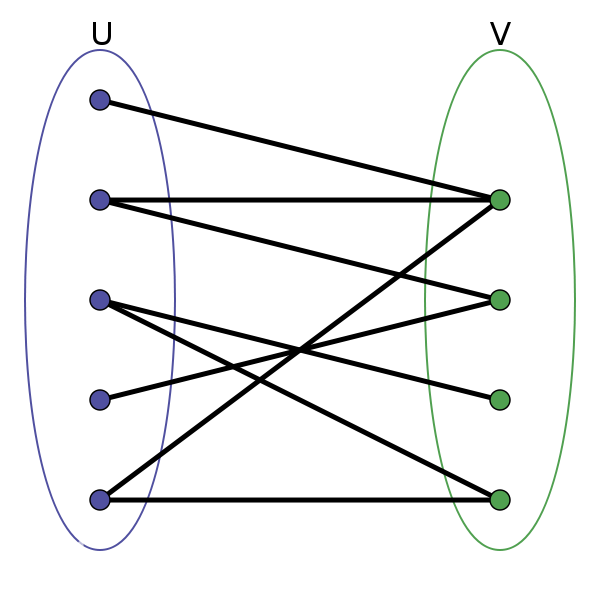
2 什么是匹配

在一个二分图$G$中选出$k$条边，组成新图$G’$，使得任意一条边的两个端点都与其他边的端点不重合，则称$G’$为$G$的一个匹配。

上图中，若$U$集编号从上至下为$1,2,3,4,5$，$V$集编号从上至下为$a,b,c,d$，则$(2,b),(5,a)$是一个匹配。

3 最大匹配

在一个二分图$G$中，匹配$G_m$的边数最大（仅考虑不带权匹配），则称$G_m$为$G$的最大匹配。

上图中，若$U$集编号从上至下为$1,2,3,4,5$，$V$集编号从上至下为$a,b,c,d$，则$(1,a),(2,b),(3,c),(5,d)$是最大匹配。

4 增广与增广路

从$U$集一未匹配点开始，找一个并$V$集的未匹配点并进行匹配（前提是有连边）的过程称为增广。
连接两个新匹配点间的边被称为增广路。

---

二 判定

二分图的判定可以有染色法解决。
因为二分图中不存在奇圈，故若用两种颜色将二分图中的每个节点染色，且使得相邻的节点颜色不同，若存在一种合法方案，就可以判定图是二分图。

用dfs模拟染色过程，一旦发现颜色冲突就跳出染色，否则返回染色成功即可。

const int CP=1e4;
const int CE=1e5;

class fs{
  public:
      int to,nxt;
}E[CE];
int hd[CP],ecnt=0;
void add(int x,int y){
    E[++ecnt].to=y;
    E[ecnt].nxt=hd[x];
    hd[x]=ecnt;
}

//paint
int col[CP]; //col[i]=0 : 未染色
             //col[i]=1 : 颜色1 
             //col[i]=-1 : 颜色2 
bool dfs(int u,int c){
    col[u] = c;
    for(int k=hd[u]; k; k=E[k].nxt){
        int to=E[k].to;
        if(col[to] == c) return false; //冲突
        if(!col[to] && !dfs(to,-c)) return false; //向下递归
    }
    return true;
}
bool examine(){
    for(int i=1;i<=n;i++)
        if(!col[i]){
            int flag = dfs(i,1);
            if(!flag) return false;
        }
    return true;
}

---

三 匈牙利算法

1 流程

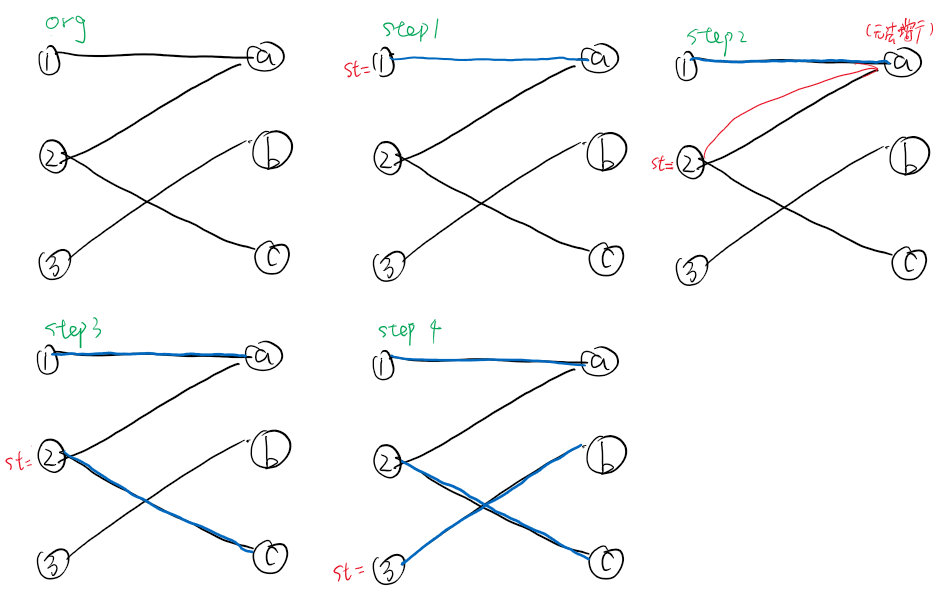
step1

以$1$为起点，找一条增广路，选中$(1,a)$（蓝线）。

step2

以$2$为起点，找一条增广路，试图选中$(2,a)$（红线）。发现$a$已被匹配，故从$2$开始，走匹配边（蓝线）到$1$，试图寻找增广路，失败。故$a$无法失配，配对失败。

此处若能寻找到增广路$(1,x)$，则$a$失配并与$2$配对，$1$重新与$x$配对，因为这样实际上增加了一条匹配边。

step 3

继续以$2$为起点，找一条增广路，选中$(2,c)$（蓝线）。

step 4

以$3$为起点，找一条增广路，选中$(3,b)$（蓝线）。
至此，左图中所有点皆以匹配完成，算法结束。

2 代码实现（match）

判断能否增广的过程需要一遍dfs，且需要知道 能(true)与否(false)。故我们需要定义一个返回值为bool的dfs。

//match
/*
节点1~n:左图节点
节点n+1~2n:右图节点
边表存图，E为边集
*/
const int CON=2e3+3;

//边表
class fs{
  public:
    int to,nxt;
}E[CON];
int hd[CON],ecnt=0;
void add(int x,int y)
{
    E[++ecnt].to=y;
    E[ecnt].nxt=hd[x];
    hd[x]=ecnt;
}

bool ins[CON]; //判断右图的节点是否已经被访问过
int mtclf[CON]; //mtclf[i]为左图节点i在右图中的匹配节点
int mtcrt[CON]; //mtclf[i]为右图节点i在左图中的匹配节点

bool dfs(int cur)
{
    for(int k=hd[cur]; k; k=E[k].nxt)
    { 
        int to=E[k].to; //to一定在右图中
        
        if(!ins[to]) //不走回头路
        {
            ins[to] = true;
            
            if(!mtcrt[to] || dfs(mtcrt[to])) //若to为没有匹配的节点，或从to节点开始可以找到新的增广路
            {
                mtclf[cur] = to; //to失配并与当前节点配对
                mtcrt[to] = cur;
                
                return true; //找到了一条增广路
            }
        }
    }
    
    return false; //无法增广
}

int match()
{
    int ret=0; //统计答案数
    
    for(int st=1; st<=n; st++) //遍历起点（左图中）
        if(!mtclf[st])
        {
            memset(ins,false,sizeof(ins));
            
            if(dfs(st))
                ret++; //每次dfs仅找到一条增广路，故答案+1
        }
            
    return ret; //返回答案
}