发表更新OI笔记18 分钟读完 (大约2681个字)

拓扑排序

对一个DAG$G=(V,E)$（$V$为点集，$E$为边集）进行拓扑排序，是将$G$中所有顶点排成一个线性序列，使得图中任意一边$(u,v)∈E$，$u$在线性序列中出现在$v$之前……

一 概念

对一个DAG $G=(V,E)$（$V$为点集，$E$为边集）进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一边$(u,v)∈E$，$u$在线性序列中出现在$v$之前。通常，这样的线性序列称为满足拓扑次(Topological Order)的序列，简称拓扑序列。

简单来说，就是找一种排序方案，使得每条边的起点总排在终点之前。
注意：一个DAG的拓扑序列不一定是唯一的。

1.1

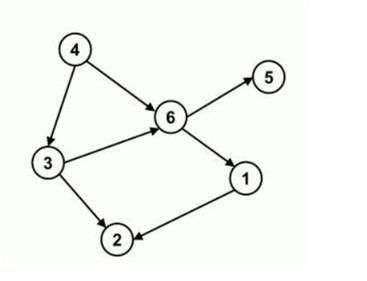
如图，合法的拓扑序列有$4,3,6,1,2,5$或$4,3,6,5,1,2$。

二 实现

1 怎么求拓扑序

要使得起点排在终点之前，那么我们首先要找到起点，即入度为$0$的节点。
然后我们删去这些点，即在图中删除以它们为起点的边。
因为DAG的特性，那么这样操作以后，新得到的图也一定是一个DAG。
于是我们可以继续找起点，删边，那么我们得到起点的顺序就是一个拓扑序。

因为DAG的性质，所以一个点不会被重复访问。

2 算法

求出一有向图的一个拓扑序。

边表

1
2
3
4
5
6
7
8
9
10
11
12
13
const int CP=1e3+3;
const int CE=CP*CP;

class fs{
    public:
        int to,nxt;
}E[CE];
int hd[CP],ecnt=0;
void add(int x,int y){
    E[++ecnt].to=y;
    E[ecnt].nxt=hd[x];
    hd[x]=ecnt;
}

排序算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
const int CP=1e3+3;
const int CE=CP*CP;

int in[CP]; //记录节点入度
int ans[CP]; //得到的拓扑序

queue<int>Q; //存放入度为0的节点

void tsort()
{
    int pos=0;
    
    for(int i=1;i<=n;i++)
        for(int k=hd[i]; k; k=E[k].nxt)
            in[E[k].to]++; //统计入度
     
    for(int i=1;i<=n;i++)
        if(!in[i])
            Q.push(i); //将起点入队
    
    while(!Q.empty())
    {
        int cur=Q.front();
        Q.pop();
        
        ans[++pos]=cur; //记录答案
        
        for(int k=hd[cur]; k; k=E[k].nxt)
        {
            int to=E[k].to;
            in[to]--; //拆边，并减少终点的入度
            if(!in[to]) //得到的是一个新起点，就把它入队
                Q.push(to);
        }
    }
}

三 建图

拓扑排序的题目中，难点一般在建图，因为建图之后求拓扑序是一件极其容易的事情。
讨论建图之前，我们先讨论一些基础的东西。

1 字典序

字符在某一标准（一般是ASCII）中出现的先后顺序叫做字典序。
类似于数字比大小，某一字符串$A$相对于字符串$B$，$A$的高位上的字符在标准中比$B$出现得早，则称$A$的字典序（相对于$B$）小。反之，则称$A$的字典序（相对于$B$）大。

若以ASCII为标准，则串$abc$比串$acb$字典序小。

设定拓扑序列中第一个元素为最高位，最后一个元素为最低位。
那么字典序小的拓扑序则是高位元素的编号尽量小，字典序大的拓扑序则是高位元素的编号尽量大。

对于第一章节中的图，拓扑序列$4,3,6,1,2,5$的字典序小，拓扑序列$4,3,6,5,1,2$的字典序大。

2 怎么求一个字典序大或小的拓扑序列

前文中给出的算法是以入队顺序确定拓扑序列。那么怎么求一个指定字典序大小的拓扑序列呢？
只需要把上文算法中的普通队列改成优先队列即可。因为在队列中的元素总是起点，在拓扑序列中的相对位置可以调换。

具体实现（重载运算符）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const int CP=1e3+3;
const int CE=CP*CP;

class node{
  public:
    int cde;
    void init(int c){cde=c;}
    
    //大字典序
    bool operator < (const node a)const
    {
        return cde<a.cde;
    }
    
    /*
    小字典序
    bool operator < (const node a)const
    {
        return cde>a.cde;
    }   
    */
};

priority_queue<node>Q;

然后照常跑拓扑排序即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int in[CP];

void tsort()
{
    int pos=0;
    
    for(int i=1;i<=n;i++)
        for(int k=hd[i]; k; k=E[k].nxt)
            in[E[k].to]++; 
     
    for(int i=1;i<=n;i++)
        if(!in[i])
        {
            node temp;
            temp.init(i);
            Q.push(temp);
        }
    
    while(!Q.empty())
    {
        node cur=Q.top();
        Q.pop();
        
        ans[++pos]=cur.cde; 
        
        for(int k=hd[cur]; k; k=E[k].nxt)
        {
            int to=E[k].to;
            in[to]--; 
            if(!in[to]) 
            {
                node temp;
                temp.init(to);
                Q.push(temp);
            }
        }
    }
}

3 例题1-建图求拓扑序

「Luogu P1983」车站分级

一条单向的铁路线上，依次有编号为$ 1, 2, …, n $的$ n $个火车站。每个火车站都有一个级别，最低为 $1$ 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 $x$，则始发站、终点站之间所有级别大于等于火车站 $x$ 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）
现有 $m$ 趟车次的运行情况（全部满足要求），试推算这 $n$ 个火车站至少分为几个不同的级别。

对于任意一趟列车，经过的站点总比没有经过的级别高，我们把级别高的站点向级别低的站点依次连边。

这样处理完$m$趟列车后，我们就会得到一个DAG。
接下来我们只需要对这个DAG进行拓扑排序。但还有一个问题，怎么求出最小级别数？
很明显，若定义排序起点的深度为$1$，那么这个最小级别数就是图中节点的最大深度。我们只需要在广搜的时候递推记录一下节点深度就可以了。

递推式：
$$\begin{aligned}f_i&=1 | i \in S \newline f_i&=\max f_i,f_j+1 | (j,i)\in E \end{aligned}$$

$S$为起点集，$E$为边集。

具体实现（仅核心算法）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const int CP=1e3+3;

int f[CP];

for(int i=1;i<=n;i++)
    if(!in[i])
    {
        f[i]=1;
        Q.push(i);
    }

while(!Q.empty())
{
    int cur=Q.front();
    Q.pop();
        
    for(int k=hd[cur]; k; k=E[k].nxt)
    {
        int to=E[k].to;
        
        f[to]=max(f[to], f[cur]+1); //here
        
        in[to]--; 
        if(!in[to]) 
            Q.push(to);
    }
}

4 反图

4-1 什么是反图？

对一个有向图$G={V,E}$，若存在一个图$G_r={V,E_r}$，其中两个图的点集相同，边集相反（定义为每一条边的方向均相反），那么称$G_r$为$G$的反图。

建立反图其实是一件非常简单的事情，只需要在节点连边的时候连反向边即可。

4-2为什么要建反图?

  • 求一个拓扑序列，使得最小的编号尽早出现。

先考虑能否用字典序解决：
字典序小使得居高位的数字尽可能小；
字典序大使得居高位的数字尽可能大。

于是我们发现，最小的字典序并不能保证最小数字尽可能靠前。

继续分析：
最小数字尽可能靠前，那么其它数字（都比它大）要尽可能靠后。
看不出什么来，那我们反过来看：最小数字尽可能靠后，那么其它数字要尽可能前。
这恰好是原图中的最大字典序（无论高位怎样排布，最大字典序会使低位尽可能小，也就是最小数字尽可能靠后）。

于是我们求一个最大字典序的拓扑序列，反过来读，就是答案吗？
不是。
就像sort一样，一段排好序的数列，反过来读（相对于排序条件）一定是无序的。

那么怎么解决这个问题？
考虑反向建图。
在原图的反图中跑最大字典序的拓扑序列。这个序列看起来是不合法的，但是反过来看就exciting了。
我们不难发现，反图中的每个拓扑序列，都是正图中的一个合法拓扑序列反转而形成的。继续考虑，求出反图中最大字典序的拓扑序列$K$，会使得最小数字在$K$中出现的尽量晚。然后我们把$K$反转形成$K_r$，那么最小数字在$K_r$中就会出现的尽可能早。然后$K_r$依然是正图的合法拓扑序列，完美解决。

4-3 算法实现

代码依然是上面的代码改了改。

边表

1
2
3
4
5
6
7
8
9
10
11
12
13
const int CP=1e3+3;
const int CE=CP*CP;

class fs{
    public:
        int to,nxt;
}E[CE];
int hd[CP],ecnt=0;
void add(int x,int y){
    E[++ecnt].to=x; //反向加边
    E[ecnt].nxt=hd[y];
    hd[y]=ecnt;
}

排序算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
const int CP=1e3+3;
const int CE=CP*CP;

class node{
  public:
    int cde;
    void init(int c){cde=c;}
    bool operator < (const node a)const
    {
        return cde<a.cde; //大字典序
    }
};

int in[CP];
int ans[CP];

prioirty_queue<node>Q;

void tsort()
{
    int pos=n; //倒着记录答案，正好是正图中的拓扑序列
    
    for(int i=1;i<=n;i++)
        for(int k=hd[i]; k; k=E[k].nxt)
            in[E[k].to]++; 
     
    for(int i=1;i<=n;i++)
        if(!in[i])
        {
            node temp;
            temp.init(i);
            Q.push(temp);
        }
    
    while(!Q.empty())
    {
        node cur=Q.top();
        Q.pop();
        
        ans[pos--]=cur.cde; //记录
        
        for(int k=hd[cur]; k; k=E[k].nxt)
        {
            int to=E[k].to;
            in[to]--; 
            if(!in[to]) 
            {
                node temp;
                temp.init(to);
                Q.push(temp);
            }
        }
    }
}

5 例题2-建立反图解决拓扑问题

「HNOI2015」菜肴制作

知名美食家小A被邀请至ATM 大酒店，为其品评菜肴。 ATM 酒店为小A准备了 N 道菜肴，酒店按照为菜肴预估的质量从高到低给予1到N的顺序编号，预估质量最高的菜肴编号为1。
由于菜肴之间口味搭配的问题，某些菜肴必须在另一些菜肴之前制作，具体的，一共有 M 条形如”i 号菜肴’必须’先于 j 号菜肴制作“的限制，我们将这样的限制简写为<i,j>。
现在，给出若干组形如<i,j>的限制，酒店希望能求出一个最优的菜肴的制作顺序，使得小A能尽量先吃到质量高的菜肴

最小编号最靠前，明显是一个反图拓扑序问题。对于每组限制<i,j>，从j向i连边，然后求最大字典序，反着输出即可。

拓扑排序

https://big-news.cn/2019/02/12/拓扑排序/

作者

ce-amtic

发布于

2019-02-12

更新于

2023-04-15

许可协议

CC BY-NC-SA 4.0

#

评论

推荐阅读

Your browser is out-of-date!

Update your browser to view this website correctly.&npsb;Update my browser now

×

×