「题解」最优贸易

C国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市……

一 题目

原题链接

描述

C国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城市的标号从 1~ n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

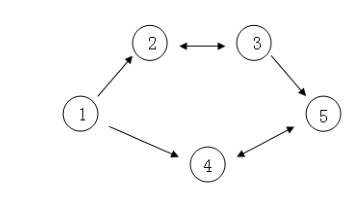
假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

假设 1~n 号城市的水晶球价格分别为 4,3,5,6,1。

阿龙可以选择如下一条线路：1->2->3->5，并在 2 号城市以 3 的价格买入水晶球，在 3 号城市以 5的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路 1->4->5->4->5，并在第 1 次到达 5 号城市时以 1 的价格买入水晶球，在第 2 次到达 4 号城市时以 6 的价格卖出水晶球，赚取的旅费数为 5。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入

第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 m 行，每行有 3 个正整数x,y,z，每两个整数之间用一个空格隔开。如果 z=1，表示这条道路是城市 x 到城市 y 之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市y 之间的双向道路。

输出

一个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 0。

---

二 题解

本题的缩点做法不好想，缩点之后的DP是个难点，在某位cy巨佬的指点下才悟出正解。

1 思路

考虑原图为DAG时的情况。

设$ val_i $为当前节点的物价，$ mn_i $为从$1$节点搜索到$i$节点的最小买入价格，$f_i$为从$1$节点到$i$节点的最大利润（不一定在$i$售出），则转移方程：
$$ f_i =\max { f_j,val_i-mn_i } | (j,i) \in E$$
也就是把状态分解成继承前面的状态（当前点不售出）和当前点售出，两者取较大值。

原图不一定为DAG，考虑使用tarjan缩点。
那么转移方程也得变一变。

考虑一个连通分量的贡献。

这个最大利润可能出自同一个连通分量，也可能出自不同。

那么它的贡献分为两类（$mx_i$表示连通分量$i$中的最大售价，$mn_i$表示连通分量$i$中的最小进价，$totmn_i$表示连通分量$1-i$中的最小进价）：

1. 最优解来自同一个连通分量。贡献为$mx_i-mn_i$。
2. 最优解来自不同的连通分量，且在当前连通分量售出物品。贡献为$mx_i-totmn_i$。
3. 最优解根当前联通分量不沾边。没有贡献并继承前面的最优解（因为状态设计的缘故，要满足无后效性）

转移方程
$$ f_i=\max { mx_i-mn_i,mx_i-totmn_i,f_j } | (j,i) \in E $$

转移需要按照拓扑序进行，再跑一遍拓扑即可。

2 实现

边表

const int CE=1e6+6;
const int CP=1e5+5;

const int INF=0x7f7f7f3f;

class fs{
  public:
      int to,nxt;
}E[CE];
int hd[CP],ecnt=0;
void add(int x,int y){
    E[++ecnt].to=y;
    E[ecnt].nxt=hd[x];
    hd[x]=ecnt;
}
void E_init(){
    memset(hd,0,sizeof(hd));
    ecnt=0;
}

缩点

//tarjan主过程
int dfn[CP],low[CP],idx=0;
int stack[CP],top=0;
bool ins[CP];

int bel[CP],mn[CP],mx[CP],scnt=0;

void tarjan(int cur)
{
    dfn[cur] = low[cur] = ++idx;
    
    stack[++top]=cur;
    ins[cur]=true;
    
    for(int k=hd[cur]; k; k=E[k].nxt)
    {
        int to=E[k].to;
        
        if(!dfn[to])
        {
            tarjan(to);
            low[cur] = min(low[cur], low[to]);
        }
        else if(ins[to])
            low[cur] = min(low[cur], low[to]); 
    }
    
    if(dfn[cur] == low[cur])
    {
        int pos;
        scnt++;
        mx[scnt]=-INF;
        mn[scnt]=INF;
        
        while(true){
            pos=stack[top--];
            ins[pos]=false;
            
            bel[pos]=scnt;
            mx[scnt] = max(mx[scnt], val[pos]);
            mn[scnt] = min(mn[scnt], val[pos]);
            
            if(pos == cur)
                break;
        }
    }
}
void scc()
{
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i);
}

//重新建图
int in[CP];

void re_build()
{
    E_init();
    
    for(int i=1;i<=m;i++)
    {
        if(bel[_x[i]] == bel[_y[i]]) //这里的_x,_y,_z都是图中边的输入数据
            continue;
            
        add(bel[_x[i]], bel[_y[i]]);
        in[bel[_y[i]]]+=1;
        
        if(_z[i] == 2){
            add(bel[_y[i]], bel[_x[i]]);
            in[bel[_x[i]]]+=1; //统计节点入度，为了跑拓扑
        }
    }
}

DP

//topo sort
int list[CP];
queue<int>Q;
void tsort(){
    for(int i=1;i<=scnt;i++)
        if(!in[i])
            Q.push(i);
    while(!Q.empty()){
        int cur=Q.front();
        Q.pop();
        list[++list[0]]=cur;
        for(int k=hd[cur]; k; k=E[k].nxt){
            in[E[k].to]--;
            if(!in[E[k].to])
                Q.push(E[k].to);
        }
    }
}

//dp
int dp()
{ 
    /*此时_x,_y已经用完，重复利用以节省空间*/
    memset(_x,0,sizeof(_x)); //_x[i] : 从scc_1到scc_i的最小买入价格 
    memset(_y,0,sizeof(_y)); //_y[i] : 从scc_1到scc_i的最大利益 
    
    tsort();
    
    /*先递推最小买入价格*/
    for(int i=1;i<=scnt;i++)
        _x[i] = mn[i];
    for(int i=1;i<=scnt;i++)
    {
        int cur=list[i];
        for(int k=hd[cur]; k; k=E[k].nxt)
            _x[E[k].to] = min(_x[E[k].to], _x[cur]);
    }
    
    for(int i=1;i<=scnt;i++)
    {
        int cur=list[i];
        for(int k=hd[cur]; k; k=E[k].nxt)
            _y[E[k].to] = max(max(_y[E[k].to], _y[cur]), //维护最优解 或 继承状态 
                              max(mx[E[k].to]-mn[E[k].to], mx[E[k].to]-_x[E[k].to]) //当前scc中的最大利益 或 当前最大价值减去之前最小差价 
                              );
            
    }
    
    return _y[bel[n]]; //返回解。注意这里的下标都是连通分量的编号
}