双连通分量

两只$\mathbf{Tarjan}$，两只$\mathbf{Tarjan}$，跑得快，跑得快……

此页面存在相关页面。关于强连通分量，请参见「强连通分量」。

一 概念

1 基本定义

无向图的双连通有两种情况：点-双连通 与 边-双连通。

• 点-双连通：若一个无向图中的去掉任意一个节点，都不会改变此图的连通性，即不存在割顶，则称作点-双连通图。 —— Baidu
• 边-双连通：若一个无向图中的去掉任意一条边，都不会改变此图的连通性，即不存在桥，则称作边-双连通图。 —— Baidu

类似与有向图的强连通分量，无向图的 点-双连通 的极大子图被称作该图的双连通分量（BiConnected Component,BCC）。而无向图的 边-双连通 的极大子图被称作该图的边-双连通分量（Edge-BiConnected Component,EBCC）。

上述还涉及到了两个概念，割顶与桥，定义如下：

• 对于一张无向图，若删去一个端点后，产生了新的连通块，则称这个端点为割顶（也称割点）。
• 对于一张无向图，若删去一条边后，产生了新的连通块，则称这条边为桥（也称割边）。

不难发现：割顶决定了点-双连通，而桥决定了边-双连通。

对于一张无向图，割顶（桥）可能不存在，也可能不仅一个。

2 图示

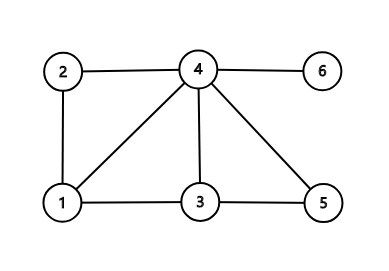
如上图，节点$4$是割顶，边$(4,6)$是桥。
图中点-双连通子图有${1,2,4}$，${1,3,4,5}$等，但BCC只有${1,2,3,4,5}$和${6}$。
类似的，边-双连通子图有${1,2,4}$等，但EBCC只有${1,2,3,4,5}$和${6}$。

---

二 割顶

在求解BCC之前，先来学习割顶的必备知识。

注：因为 桥和边-双连通 与 点-双连通 有许多相似之处，故不重点说明。
以下所有 “双连通/双连通子图/双连通分量/BCC” 等均指 “点-双连通”。

1 dfs树

dfs树的基本内容在SCC算法分析中已经讲过，这里不再过多重复，只对部分概念做必要说明。

• 树边：dfs所经过的边
• 返祖边：连接子节点与它的祖先节点的边，本质上与树边无异

注意：无向图的dfs树上不存在横叉边。

可以绘制出上图的dfs树：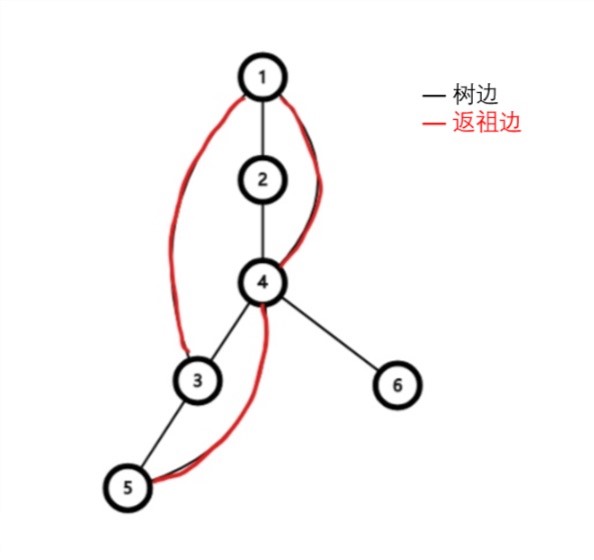

2 定理

我们先来推导一下割顶的基本判定方法。

猜想：

• 在一个无向图中，若$u$是割顶，当且仅当$u$存在一个子节点$v$，使得子树$v$内没有边返回$u$的祖先。

画出图来就长这样：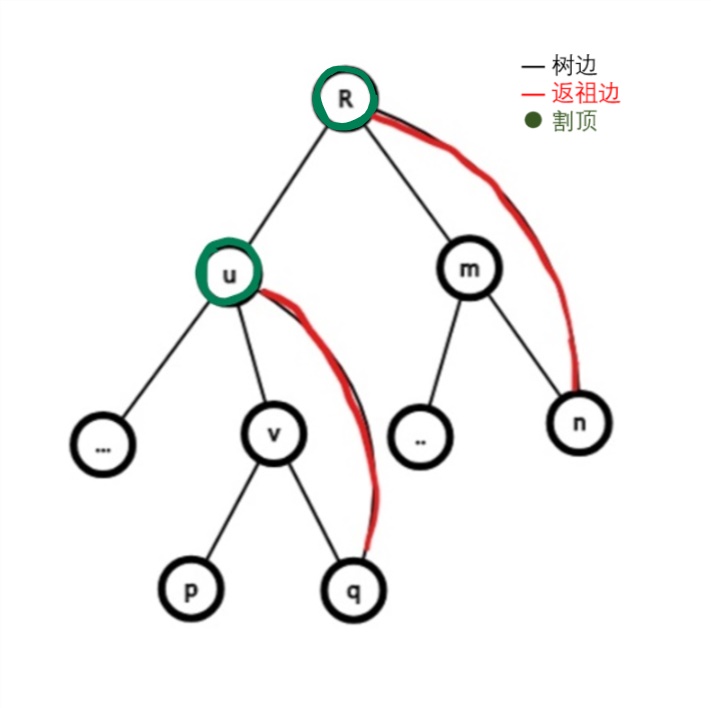

看上去很对，但是有疏漏。

根节点很特殊。一定没有返祖边指向根的祖先，因为根没有祖先。但是仅当根由两棵及以上的子树时，根才是割点，否则删去它并不影响图的连通。
所以需要特判根。

2-1 割顶的判定定理

1. 根节点是割顶，当且仅当在dfs树上它有两个及以上的子节点。
2. 非根节点$u$是割顶，当且仅当在dfs树上$u$存在一个子节点$v$，使得子树$v$内没有返祖边返回$u$的祖先。

简单证明：

1. 此时删去根节点会让它的各个子树互不连通，因为不存在横叉边。
2. 此时删去$u$，会使得子树$v$中的节点“独立”出来，形成新的连通块。

2-2 桥的判定定理

与上面的类似。

• 对于任意节点$u$，若$u$存在一个子节点$v$，使得子树$v$内没有返祖边返回**$u$及$u$的祖先**，则边$(u,v)$是桥。

图示如下：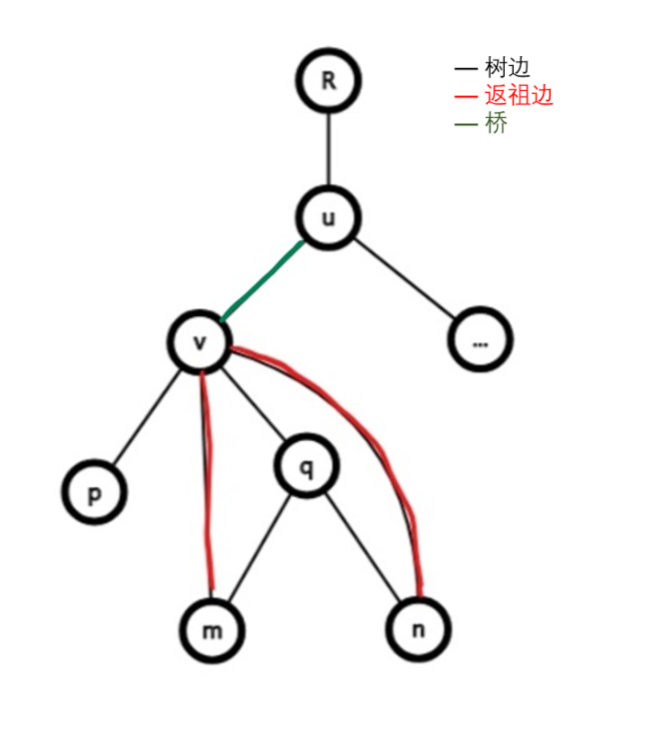

证明其实挺好想：删掉这条边会孤立子树$v$。

3 算法

该算法由Robert Tarjan提出（又是他）。

3-1 思路

设节点$u$被dfs到的次序号是$dfn[u]$，从它能到达的祖先的最小次序号是$low[u]$，那么定理中的第二条就变成了：

• 找一个节点$u$，使得$low[v] \geqslant dfn[u] | (u,v)\in E$，则判定$u$是割顶。

同理，桥的判定定理可以表示为：

• 找一个节点$u$，使得$low[v] > dfn[u] | (u,v)\in E$，则判定无向边$(u,v)$是桥。

于是可以在dfs一张无向图的时候求解。

3-2 流程

该算法主要有以下四步：

1. dfs整个图。
2. 对于每个非根节点，使用子节点的$low$值更新当前节点的$low$值。
3. 访问该节点出发的所有返祖边，并用这条边指向的祖先的$dfn$值更新当前节点的$low$值。注意一定是$dfn$值，下面会讲。
4. 判定是否是割顶（用到上面的不等式）。

对于1-2中的图，可以得到如下的一张dfs树（桥和割顶都已经标出）。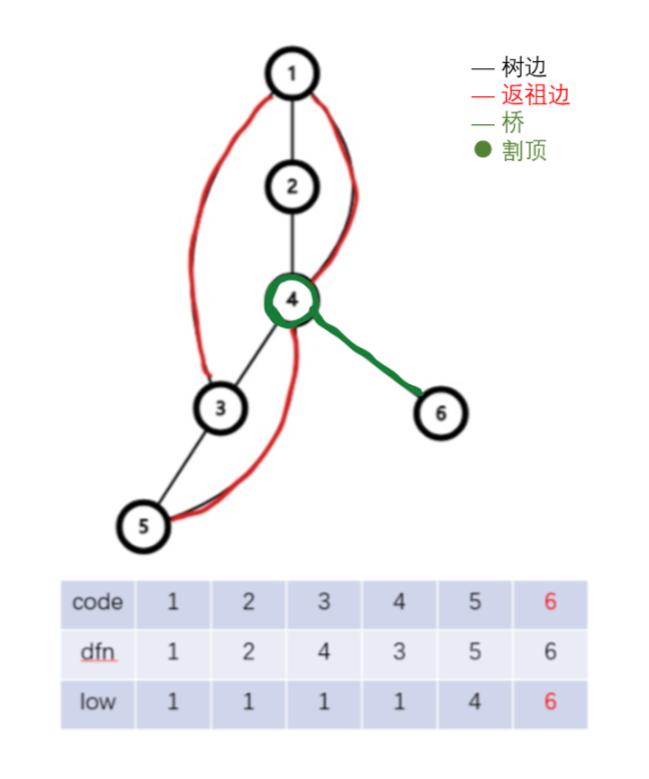

发现存在$low[6]\geqslant dfn[4]$，故判定$4$是割顶。

小问题：为什么一定是dfn值？

看下面的图。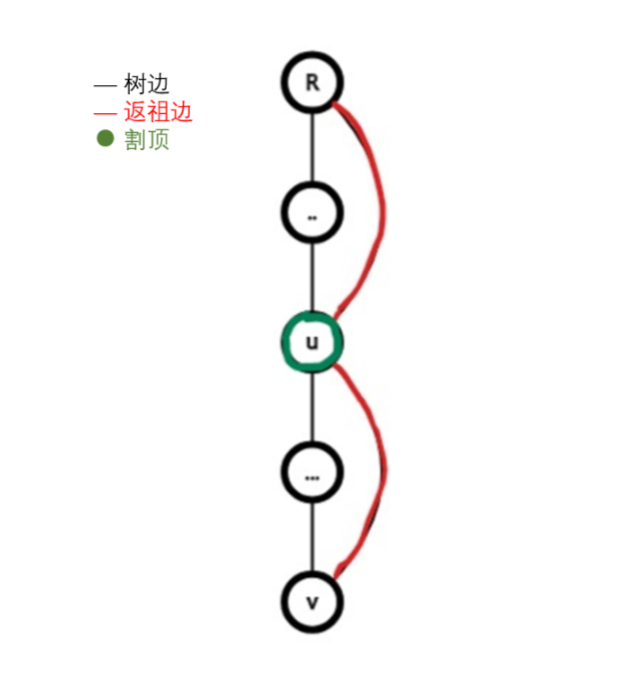

此时使用$low[u]$更新$low[v]$，实际上走了两条返祖边。则会判定$u$不是割顶，但实际上它是。

3-3 代码

割顶的求解如下：

const int CP=1e3+3;
const int CE=CP*CP;

//边表
class fs{
    public:
        int to,nxt;
}E[CE];
int hd[CP],cnt=0;
void add(int x,int y)
{
    E[++cnt].to=y;
    E[cnt].nxt=hd[x];
    hd[x]=cnt;
}

//cut
int dfn[CP],low[CP];
int idx=0;

bool iscut[CP]; //是否是割顶

void tarjan(int cur,int prv)
{
    int child = 0; //孩子数，用于根的特判
    
    dfn[cur] = low[cur] = ++idx; //设置初始值
    
    for(int k=hd[cur]; k; k=E[k].nxt)
    {
        int to=E[k].to;
        
        if(!dfn[to]) //是树边
        {
            child++;
            tarjan(to,cur); //向下搜索
            
            low[cur] = min(low[cur], low[to]); //更新
            
            if(low[to] >= dfn[cur]) //用儿子来判定
                iscut[cur]=true;
        }
        else if(to != prv) //是返祖边
            low[cur] = min(low[cur], dfn[to]); //更新
    }
    
    if(!prv && child==1) //处理根
        iscut[cur]=false; 
}

void bcc() //主求解函数
{
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,0);
}

桥的求解如下：

因为边表没法有效地一次性保存双向边。所以边的下标从$1$开始，使得$k \text{ xor } 1$就是$k$的反向边。（$k$与$k \text{ xor } 1$共同组成一条无向边）。

const int CP=1e3+3;
const int CE=CP*CP;

//边表
class fs{
    public:
        int to,nxt;
}E[CE];
int hd[CP],cnt=1; //从1开始
void add(int x,int y)
{
    E[++cnt].to=y;
    E[cnt].nxt=hd[x];
    hd[x]=cnt;
}

//bridge
int dfn[CP],low[CP];
int idx=0;

bool isbri[CE]; //是否是桥

void tarjan(int cur,int prv)
{
    dfn[cur] = low[cur] = ++idx; 
    
    for(int k=hd[cur]; k; k=E[k].nxt)
    {
        int to=E[k].to;
        
        if(!dfn[to]) 
        {
            tarjan(to,cur); //向下搜索
            
            low[cur] = min(low[cur], low[to]); 
            
            if(low[to] > dfn[cur]) //判定
                isbri[k] = isbri[k^1] = true;
        }
        else if(to != prv)
            low[cur] = min(low[cur], dfn[to]); 
    }
}

void ebcc() //主求解函数
{
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,0);
}

---

三 算法实现

1 BCC

学会了求解割顶，求出BCC就再容易不过了。

维护一个栈，栈内保存每一次走过的边（一定保存边，因为两个不同的双连通子图可能有交点，但一定没有交边）。每当发现割顶时，出栈，直到发现当前出栈的边恰好是连接割顶与判定它的子节点的边。则出栈的所有边同属一个双连通子图，这些边的端点也同属一个双连通子图。

代码如下：
因为回溯到根的时候，剩余栈内元素一定是一个双连通子图，故先出栈再特判根。

const int CP=1e3+3;
const int CE=CP*CP;

//边表
class fs{
    public:
        int from,to,nxt;
}E[CE];
int hd[CP],cnt=0;
void add(int x,int y)
{
    E[++cnt].from=x;
    E[cnt].to=y;
    E[cnt].nxt=hd[x];
    hd[x]=cnt;
}

//bcc
int dfn[CP],low[CP];
int idx=0;

int bel[CP],bcnt=0; //每个点所属的bcc编号，为-1则表示该点是割顶（割顶同时属于两个bcc，所以它的bel无意义）
int stack[CE],top=0;

void tarjan(int cur,int prv)
{
    int child = 0; 
    
    dfn[cur] = low[cur] = ++idx; 
    
    for(int k=hd[cur]; k; k=E[k].nxt)
    {
        int to=E[k].to;
        
        if(!dfn[to]) 
        {
            child++;
            stack[++top]=k; //入栈
            tarjan(to,cur); //向下搜索
            
            low[cur] = min(low[cur], low[to]); 
            
            if(low[to] >= dfn[cur]) //是割顶
            {
                  int pos;
                  ++bcnt;
                  while(true)
                  {
                      pos=stack[top--]; //出栈
                      bel[E[pos].from] = bel[E[pos].to] = bcnt;
                      if(E[pos].from==cur && E[pos].to==to) //发现当前的树边
                           break;
                  }
                bel[cur] = -1; //标记割顶
            }
        }
        else if(to != prv)
            low[cur] = min(low[cur], dfn[to]); 
    }
    
    if(!prv && child==1) //处理根
        bel[cur] = bcnt;
}

void bcc() //主求解函数
{
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,0);
}

2 EBCC

EBCC可以用更简单的两遍dfs求出：

第一遍dfs在图上删去所有的桥。第二遍dfs求出这之后所有的连通块。
那么每个连通块都是一个边-双连通子图。

---

四 BCC可以解决什么样的问题？

噫，好了，我中了，我们已经学会了BCC。
但是BCC可以用来求解什么样的问题呢？

在这里梳理一下BCC的主要性质：

1. 一个BCC一定是若干个简单环（环上的边数等于点数）的并。求出BCC的主要目的就是求出图上的若干环。
2. 根据双连通（也是环的性质）可知：同一双连通子图中的点一定有至少两条路径可达。
3. 两个不同的双连通子图的交点一定是该图的割顶，或这个点不存在。