悬线法

有边界限制的最大子矩阵问题一般可以通过悬线法（玄线法）解决，即通过处理出每个节点可以向四周扩张的长度，来计算包含该节点的最大矩阵面积……

一 模型

1 最大子矩阵问题

最大子矩阵问题，通常是指在一个$n\times m$的矩阵中，除去若干不能被包含的点（障点），找出一个面积最大的子矩阵。

2 悬线

从矩阵中的一个格点出发，到某一障点引一条竖直的线段被称作悬线。广义的悬线可以被理解为从格点到障点竖直或水平的线段。

3 定义与递推

对于每个格点$(i,j)$，定义三种变量如下：

1. $l_{i,j}$：格点$(i,j)$的向左端的悬线长度。
2. $r_{i,j}$：格点$(i,j)$的向右端的悬线长度。
3. $up_{i,j}$：格点$(i,j)$的向上的悬线长度。

这些数据可以通过递推处理出来。当$(i,j)$不是障点时（障点的悬线长度均为$0$），有以下递推式：
$$ l_{i,j} = l_{i,j-1}+1 \newline r_{i,j} = l_{i,j+1}+1 \newline up_{i,j} = up_{i-1,j}+1 $$

4 数据的处理

通过这些数据，我们就可以得出经过格点$(i,j)$的最长宽度（$l_{i,j}+r_{i,j}-1$）和最大高度（$up_{i,j}$）。但是仅凭这些数据还不能得出正确答案。

看下面的图：

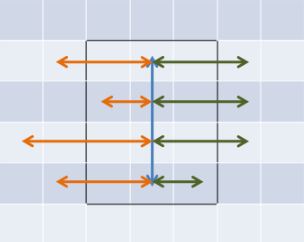
不难发现，当前包含该节点的最大子矩阵（实线框出）面积，与橙色线段和绿色线段中长度最小的那两个有关。
也就是说当前得到的面积应该表示为：
$$ S_{max} = up_{i,j}(\min\limits_{i-up_{i,j}< k\leqslant i} l_{k,j} + \min\limits_{i-up_{i,j}< k\leqslant i} r_{k,j} -1)$$

其中这两个$\min$值也是可以直接递推出来的。即当上方格点不是障点时，令$l_{i,j} = \min l_{i,j},l_{i-1,j}$，那么实际上满足了$l_{i,j} =\min\limits_{i-up_{i,j}< k \leqslant i} l_{k,j} $。$r_{i,j}$同理。

那么当递推完成时，该面积为：
$$ S_{max} = up_{i,j}(l_{i,j} + r_{i,j} -1)$$
预处理之后，枚举每个格点，用上面的式子算面积，取最大值就好了。

---

二 代码

总共需要有三遍递推，每遍复杂度均为$O(nm)$，总复杂度$O(nm)$。模板题目。

const int CN=1e3+3;

bool G[CN][CN];
int n,m;

int up[CN][CN],l[CN][CN],r[CN][CN];

for(int i=1;i<=n;i++){ //第一遍递推处理初值
        for(int j=1;j<=m;j++)
            if(G[i][j]) l[i][j] = l[i][j-1]+1;
        for(int j=1;j<=m;j++)
            if(G[i][j]) up[i][j] = up[i-1][j]+1;
        for(int j=m;j;j--)
            if(G[i][j]) r[i][j] = r[i][j+1]+1;
    }
for(int i=2;i<=n;i++) //第二遍递推求出min值
    for(int j=1;j<=m;j++)
        if(G[i][j] && G[i-1][j]){
            l[i][j] = min(l[i][j], l[i-1][j]);
            r[i][j] = min(r[i][j], r[i-1][j]);
        }
            
int ans=0;
for(int i=1;i<=n;i++) //第三遍遍历求出答案
    for(int j=1;j<=n;j++)
        ans = max(ans, (l[i][j]+r[i][j]-1)*up[i][j]);

---

三 变形

「ZJOI2007」棋盘制作

国际象棋是世界上最古老的博弈游戏之一，和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想，棋盘是一个8×8大小的黑白相间的方阵，对应八八六十四卦，黑白对应阴阳。
而我们的主人公小Q，正是国际象棋的狂热爱好者。作为一个顶尖高手，他已不满足于普通的棋盘与规则，于是他跟他的好朋友小W决定将棋盘扩大以适应他们的新规则。
小Q找到了一张由N×M个正方形的格子组成的矩形纸片，每个格子被涂有黑白两种颜色之一。小Q想在这种纸中裁减一部分作为新棋盘，当然，他希望这个棋盘尽可能的大。
不过小Q还没有决定是找一个正方形的棋盘还是一个矩形的棋盘（当然，不管哪种，棋盘必须都黑白相间，即相邻的格子不同色），所以他希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积，从而决定哪个更好一些。
于是小Q找到了即将参加全国信息学竞赛的你，请编程输出可以找到的最大正方形棋盘和最大矩形棋盘的面积。

这题中没有“障点”，那么悬线应该定义为“从某一格点开始沿竖直或水平方向所能走出的最长的黑白相间的道路”。依然按照上面的方法处理即可，细节参见代码。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;

const int CN=2e3+3;

int read(){
    int s=0,ne=1; char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') ne=-1;
    for(;c>='0'&&c<='9';c=getchar()) s=(s<<1)+(s<<3)+c-'0';
    return s*ne;
}

bool G[CN][CN];
int n,m;

int up[CN][CN],l[CN][CN],r[CN][CN];

int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            int c=read();
            G[i][j] = c ? true : false;
            l[i][j] = r[i][j] = up[i][j] = 1;
        }
    
    //preparation
    for(int i=1;i<=n;i++){
        for(int j=2;j<=m;j++)
            if(G[i][j] != G[i][j-1]) //不同时转移
                l[i][j] = l[i][j-1]+1;
        for(int j=m-1;j;j--)
            if(G[i][j] != G[i][j+1]) 
                r[i][j] = r[i][j+1]+1;
    }
    for(int i=2;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(G[i][j] != G[i-1][j]) 
                up[i][j] = up[i-1][j]+1;
    for(int i=2;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(G[i][j] != G[i-1][j]){ //求出min值
                l[i][j] = min(l[i][j], l[i-1][j]);
                r[i][j] = min(r[i][j], r[i-1][j]);
            }
            
    //solve
    int ans = 0;
    for(int i=1;i<=n;i++) //正方形 
        for(int j=1;j<=m;j++){
            int a = min(up[i][j], (l[i][j]+r[i][j]-1)); //从两个边长里面取一个小的
            ans = max(ans, a*a);
        }
    printf("%d\n",ans);
    ans = 0;
    for(int i=1;i<=n;i++) //矩形
        for(int j=1;j<=m;j++)
            ans = max(ans, (l[i][j]+r[i][j]-1)*up[i][j]);
    printf("%d",ans);
    
    return 0;
}