「题解」Atlantis

矩阵面积并问题：扫描线法+线段覆盖……

一 题目

Source

Descriptions

There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.

Input

The input file consists of several test cases. Each test case starts with a line containing a single integer n (1<=n<=100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0<=x1<x2<=100000;0<=y1<y2<=100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.

The input file is terminated by a line containing a single 0. Don’t process it.

Output

For each test case, your program should output one section. The first line of each section must be “Test case #k”, where k is the number of the test case (starting with 1). The second one must be “Total explored area: a”, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.

Output a blank line after each test case.

---

二 题解

题目大意

二维平面内有n个矩形，有些矩形两两相交。给出矩形主对角线的两个端点的坐标（可能不是整数），试求矩形所覆盖的总面积。

思路

扫描线法
假设我们有一条平行于y轴的线段，从y轴开始不断向x轴正方向平移。我们可以根据这条线段把这个若干矩形组成的不规则图形划分成若干部分（实际上是根据每个矩形平行于y轴的那些边），如下图：

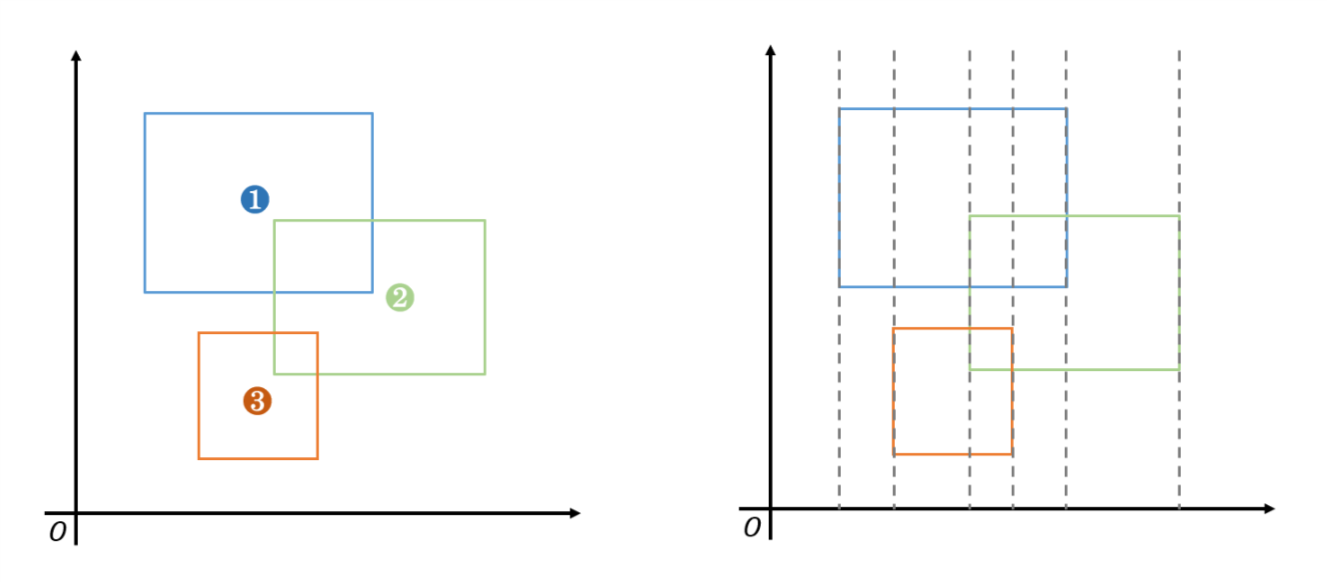
这样划分，那么每两条相邻的扫描线之间的图形面积就可以快速的求出，因为这部分图形都是矩形，且有相同的宽（即两条扫描线之间的距离）。
那么我们只需要求出图形的高之和，也就是若干条线段的并。

线段覆盖
如下图，两条扫描线之间的部分是两个不相交的矩形，它们的并的面积可以用下面的式子求出。

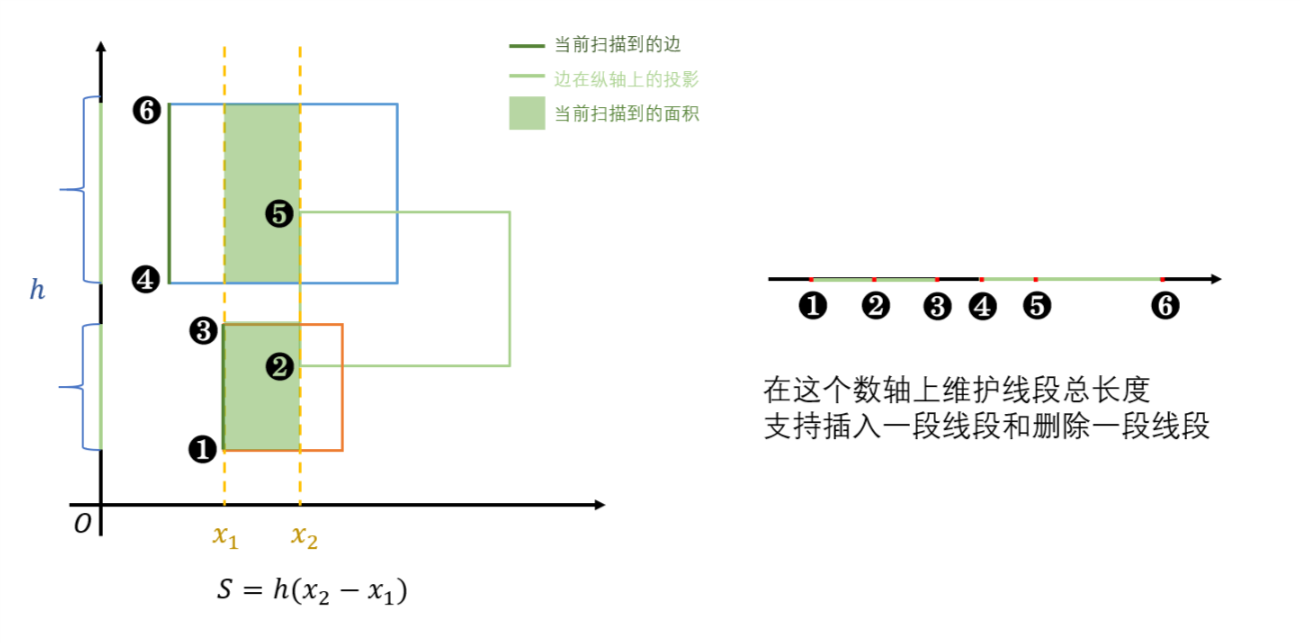
$(x_2-x_1)$这个值实际上枚举扫描线就可以确定，关键是求出$h$的值。单看$h$在y轴上的投影（图二），不难发现$h$是若干线段的并。于是我们不妨这样想：把每个矩形看成两条相等的线段（高），那么我们在扫描的过程中会先后遇到这两条线段。第一次遇到时，我们在y轴上投影这条线段（也可以看成把它覆盖在y轴上），第二次遇到时，我们把这条线段从y轴上删除。于是我们只需要求出某一时刻，在y轴上的所有线段之并就好了。

那么实际上我们要维护这样一个东西：维护若干线段的并的长度，支持删除或插入一段线段。

那么就可以引入“线段覆盖”这个概念。实际上就是一棵节点维护的是一条“线段”的线段树，树上的每个节点维护在某个区间$[l,r]$内被覆盖的线段长度。详细定义如下：

class node{ 
  public:
    int l,r; //节点所维护的区间
    int cnt; //这个区间被完全覆盖的次数
    int len; //这个区间被覆盖的长度
}

如下图，每条线段两头的标号代表节点所维护的线段的两个端点（离散化之后）：

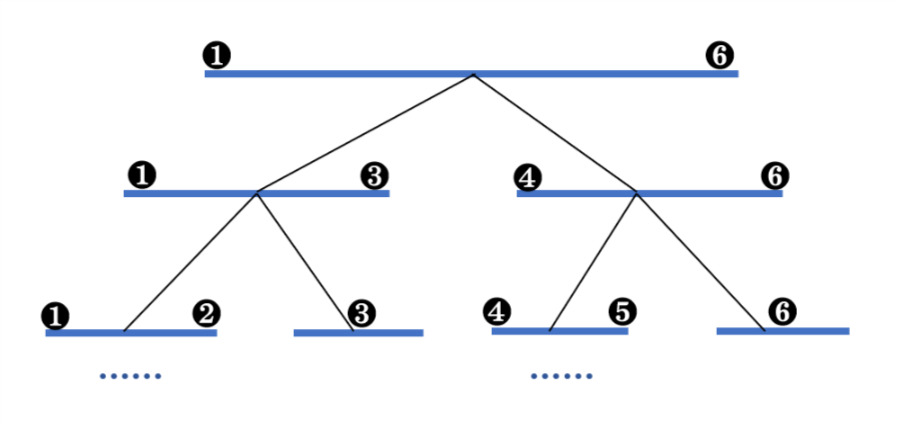
不难发现线段是满足“区间加法”的性质的，因为在合并时，父区间若未被完全覆盖，则父区间维护的线段长度一定是子区间维护值的和，否则就是子区间的覆盖长度之和。另外还需要对线段的端点进行离散化，细节参见代码。

细节

坐标是可能有小数的，因此需要离散化，详见代码。

其次，因为线段树上的每段区间只能划分成$[l,mid]$和$[mid+1,r]$这两个子区间，否则会无限递归。但是如果把 所维护线段的端点 和 线段树的端点 设定为一个点，实际上$[mid,mid+1]$这个区间是被扔掉了的。因此我们若要修改$[l,r]$区间的值，必须调用递归修改$[l,r-1]$区间，然后在回溯更新区间大小的时候，按照$[l,r]$区间更新就好了，正确性请自行验证。

代码：

#include<iostream> 
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;

#define DB double

int read(){
    int s=0,ne=1; char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') ne=-1;
    for(;c>='0'&&c<='9';c=getchar()) s=(s<<1)+(s<<3)+c-'0';
    return s*ne;
}

const int CN = 2010;

class segment{ //定义一条线段
  public: DB l,r,x; 
    int f; //线段的值(1或-1) 
    /*矩形的对边的值分别为1 -1，这样当扫描完这个矩形的时候，这两条线段会抵消掉*/
    bool operator < (const segment& a)const 
    {return x < a.x;}  //按横坐标排序
}s[2*CN];

int n,scnt = 0,pcnt = 0; //线段的数量:scnt 离散化后点的数量:pcnt
DB pos[2*CN],ans; //pos:离散化后每个点对应的原始值 ans:面积和

class node{ //定义线段树的一个节点
  public: DB len; //被覆盖的长度
      int cnt;  //是否被整段覆盖 (被整段覆盖的次数)
};
class st{ //线段树
  public:
      node d[8*CN];
      inline void build(int l,int r,int k){ //建树
          d[k].cnt = 0; d[k].len = 0; //没有被覆盖
          if(l == r) return;
          int m = (l+r)>>1;
          build(l,m,k<<1);
          build(m+1,r,k<<1|1);
    }
    DB get_len(int l,int r,int k){ //更新线段长度
        if(d[k].cnt) return pos[r+1]-pos[l]; //被整段覆盖，r要+1
        if(l == r) return 0; //不是线段
        return d[k<<1].len + d[k<<1|1].len; //子区间求和
    }
    inline void modify(int l,int r,int k,int s,int t,int x){ //修改
        if(s<=l && r<=t){ //被包含
            d[k].cnt += x; //更新覆盖情况
            d[k].len = get_len(l,r,k); //更新
            return;
        }
        //不被包含
        int m = (l+r)>>1;
        if(s <= m) modify(l,m,k<<1,s,t,x);
        if(m < t) modify(m+1,r,k<<1|1,s,t,x);
        d[k].len = get_len(l,r,k); //更新
    }
}sgt;

int main()
{
    n = read();
    int kase = 0;
    while(n){
        ans = 0; scnt = 0;
        
        for(int i=1;i<=n;i++){
            DB x1,y1,x2,y2;
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            //初始化线段
            s[scnt+1].l = s[scnt+2].l = min(y1,y2);
            s[scnt+1].r = s[scnt+2].r = max(y1,y2);
            s[scnt+1].x = x1; s[scnt+2].x = x2;
            s[scnt+1].f = 1; s[scnt+2].f = -1;
            pos[scnt+1] = y1; pos[scnt+2] = y2;
            scnt += 2;
        }
        
        //离散化 
        sort(s+1,s+scnt+1); //把线段排序
        sort(pos+1,pos+scnt+1); //把离散化的查询表排序 
        pcnt = 1;
        for(int i=2;i<=scnt;i++)
            if(pos[i] != pos[i-1])
                pos[++pcnt] = pos[i];
        
        //建树
        sgt.build(1,pcnt,1); 
        for(int i=1;i<=scnt;i++){
            int l = lower_bound(pos+1,pos+pcnt+1,s[i].l)-pos; //查找离散化之后的值
            int r = lower_bound(pos+1,pos+pcnt+1,s[i].r)-pos-1; //r要-1
            sgt.modify(1,pcnt,1,l,r,s[i].f);
            ans += (s[i+1].x-s[i].x)*sgt.d[1].len; //统计答案
        }
        
        printf("Test case #%d\nTotal explored area: %.2lf\n\n",++kase,ans);
        
        n = read();
    }
    
    return 0;
}