发表更新OI笔记28 分钟读完 (大约4260个字)

树链剖分

树链剖分是一种针对树上问题的很优秀的处理想法。准确的说，它就是一种把“树”映射成“链”的想法。而对于“链”，我们能进行很多处理，诸如挂上线段树，维护前缀和之类。通过这些优秀的数据结构，我们就可以很好的解决有关树上路径的诸多问题……

一 引入

1 模型

对于区间求和、区间最值问题，我们有一个很好的数据结构模型——线段树来解决。
但是如果我们把区间换成在一棵树上呢？

维护一棵树，树上的每个点都有一个权值，支持修改树上任意一个点对的路径上，所有点的权值和以任意一个节点为根的子树上所有点的权值，查询任意一个点对的路径上的权值和和以任意一个节点为根的子树上的权值和

怎样解决？
这时就需要引入“树链剖分”这一概念，即破树为链，再在链上维护线段树。

还有一类问题，是维护树上的边权。不难发现树上除根以外的所有节点 和 它的父节点的边总是唯一的，那么我们可以把边权看作点权，也就是让$v$的点权等于$u\to v$的边权（$u$是$v$的父节点），再修改一下细节就好了。

2 概念

学习树链剖分需要先引入几个概念：

  • 重儿子（$\text{prv}[i]$）：节点$i$的子节点中，子树大小最大的那一个。
  • 重链：一个节点的重儿子，重儿子的重儿子，……，组成的链。
  • $\text{sz}[i]$：以节点$i$为根的子树的大小（节点数量）。
  • $\text{prv}[i]$：节点$i$的父节点。
  • $\text{dep}[i]$：节点$i$在树上的深度（定义根的深度为$1$）。
  • $\text{pos}[i]$：节点$i$映射在线段树上的节点编号，编号按照dfs的先后顺序从小到大编排。
  • $\text{tid}[i]$：线段树上的节点$i$映射在原树上的节点编号，与$\text{pos}[i]$互为反函数。
  • $\text{top}[i]$：节点$i$所在的重链上，深度最低的那个节点（也可以看作重链的根）。

如下图，标记出了一棵树上的所有重链（注意，每个节点都必定在一条重链上）与重链的根，每个节点的重儿子，节点的深度、子树大小和编号（$\text{pos}[i]$）。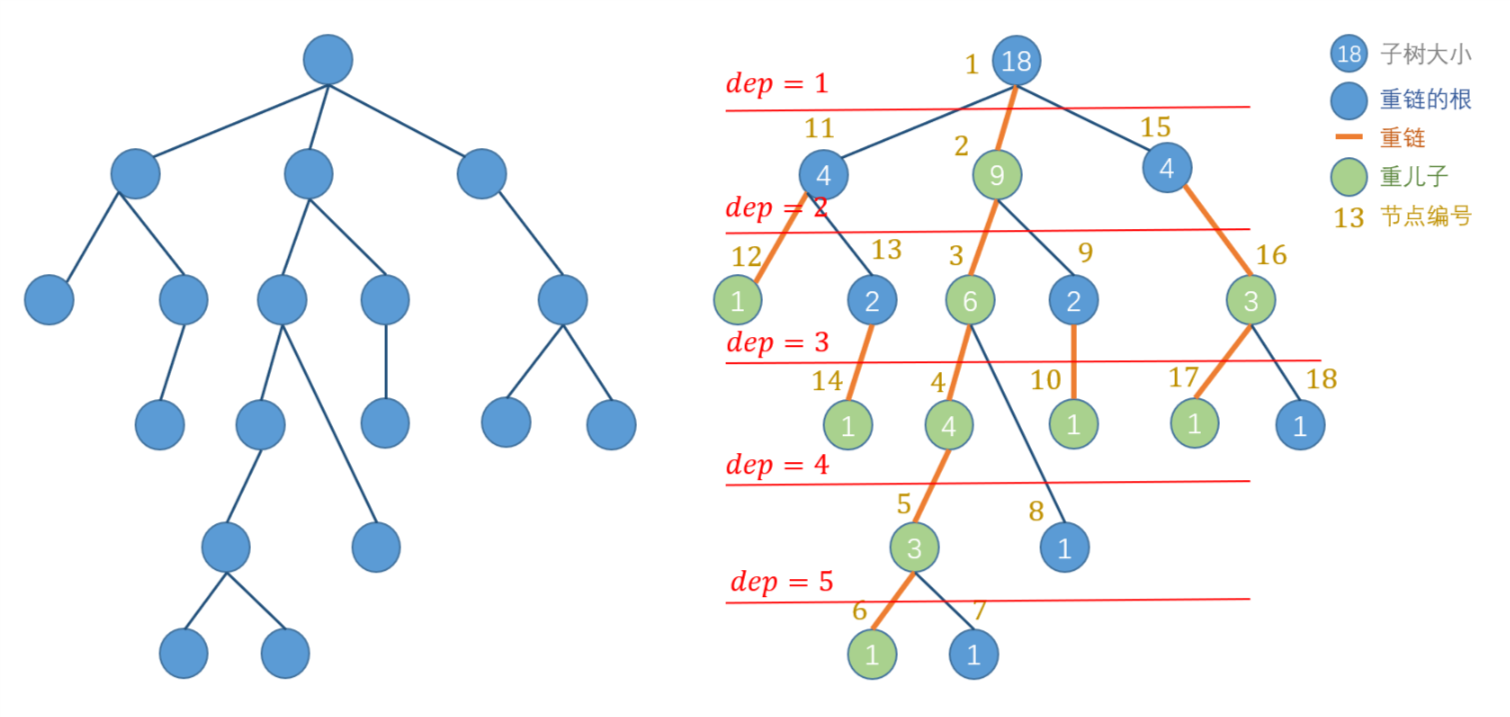
一.2(1) 图解树链剖分

注意：我们对节点进行编号的时候，优先dfs遍历当前节点的重儿子，这样就可以保证一条重链上的编号总是连续的。

二 实现

1 思想

那么怎么实现上面的问题呢？

在处理出节点的dfs编号之后，我们不妨把这$n$个编号当作区间，把每条重链映射在这个区间上，如下图：
二.2(2) 重链分布在区间上

显然我们可以用线段树去维护这个区间，然后我们就可以快速的求出一条重链上任意一个点对间所有点的权值和。

跳链操作

不在一条重链上呢？
不妨这样想：我们不断让所在重链的深度（定义为链的根的深度）大的那个点每次跳到它所在重链的根的父节点，也就是另一条重链上。这样，最后总能让这两个点位于一条重链上。
那么我们只需要在节点每条过一条重链时，记录这条重链上所有点的权值和，然后再加上最后在同一重链上是两点间的点权和，就是两点的路径上所有点的权值之和。关于权值和修改的问题也同理。

子树查询

再看修改子树上的所有点权和这个操作。
不难发现以$i$为根的子树，点编号的范围是$[i,i+\text{sz}[i]-1]$。那么只需要在线段树上直接区间修改就好了。

这样，我们就可以在最高$O((log_2)^2n)$的时间里，完成一次 修改/查询 操作。

2 代码

预处理：两遍dfs，分别处理出$\text{prv}[i],\text{sz}[i],\text{prv}[i],\text{dep}[i]$和$\text{pos}[i],\text{tid}[i],\text{top}[i]$。

然后建立线段树，并写好跳链操作就好了。

代码：
模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
const int CN = 2e6+10;

class fs{ //边表
  public:
      int to,nxt;
      void init(int t,int n) {to=t; nxt=n;}
}E[CN<<2];
int hd[CN],ecnt = 0;
void add(int x,int y){
    E[++ecnt].init(y,hd[x]);
    hd[x] = ecnt;
}

//v define
int n,m,r,R; //题目要求答案对R取余
int v[CN]; //点权

/*SGT*/
/*Segment Tree 线段树 习惯简写SGT*/
int dep[CN]; //节点深度 
int sz[CN];  //以节点为根的子树的大小 
int imp[CN]; //节点的重儿子 
int pos[CN]; //节点编号映射在线段树上的编号
int tid[CN]; //线段树上节点编号映射到节点实际编号 
int top[CN]; //节点所在重链的根 
int prv[CN]; //节点的父亲节点 
//初始化函数 
void init1(int u){
    dep[u] = dep[prv[u]]+1; //深度
    sz[u] = 1; //子树大小
    int mx = 0; //记录最大的子树大小
    for(int k=hd[u]; k; k=E[k].nxt){
        int v = E[k].to;
        if(!dep[v]){
            prv[v] = u;
            init1(v);
            sz[u] += sz[v];
            if(sz[v] > mx) mx = sz[imp[u] = v]; //更新重儿子
        }
    }
}
int idx = 0; //编号 
void init2(int u,int t){ 
    pos[u] = ++idx; //更新编号
    tid[idx] = u; 
    top[u] = t; //维护链的根
    if(!imp[u]) return; //叶节点
    init2(imp[u], t); //优先访问重链 
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(v!=imp[u] && dep[v]>dep[u]) init2(v, v); //新开一条重链 
    }
}
//线段树 
class SegmentTree{
  public: int d[CN<<2],tag[CN<<2];
    void build(int l,int r,int k){ //构造
        if(l == r) return (void)(d[k] = v[tid[l]]%R);
        int m = (l+r)>>1;
        build(l,m,k<<1);
        build(m+1,r,k<<1|1);
        d[k] = (d[k<<1]+d[k<<1|1])%R;
    }
    void PushDown(int l,int r,int m,int k,int s,int t){ //标记下传
        (d[k<<1] += tag[k]*(m-l+1)) %= R; (tag[k<<1] += tag[k]) %= R;
        (d[k<<1|1] += tag[k]*(r-m)) %= R; (tag[k<<1|1] += tag[k]) %= R;
        tag[k] = 0;
    }
    void modify(int l,int r,int k,int s,int t,int x){ //修改
        if(s<=l && r<=t){
            (d[k] += x*(r-l+1)) %= R; (tag[k] += x) %= R;
            return;
        }
        int m = (l+r)>>1;
        if(tag[k]) PushDown(l,r,m,k,s,t);
        if(s <= m) modify(l,m,k<<1,s,t,x);
        if(m < t) modify(m+1,r,k<<1|1,s,t,x);
        d[k] = (d[k<<1]+d[k<<1|1])%R;
    }
    int query(int l,int r,int k,int s,int t){ //查询
        if(s<=l && r<=t) return d[k];
        int m = (l+r)>>1,rec = 0;
        if(tag[k]) PushDown(l,r,m,k,s,t);
        if(s <= m) rec += query(l,m,k<<1,s,t);
        if(m < t) rec += query(m+1,r,k<<1|1,s,t);
        return rec%R;
    }
}sgt;
//跳链函数 
void PathModify(int u,int v,int x){ //路径修改
    x %= R;
    while(top[u] != top[v]){ //跳至同一条链
        if(dep[top[u]] > dep[top[v]]) swap(u,v);
        sgt.modify(1,n,1,pos[top[v]],pos[v],x); //修改
        v = prv[top[v]]; //让深度大的向上跳
    }
    sgt.modify(1,n,1,min(pos[u],pos[v]),max(pos[u],pos[v]),x);
}
void SubTreeModify(int u,int x){ //子树修改
    x %= R;
    sgt.modify(1,n,1,pos[u],pos[u]+sz[u]-1,x); //直接修改
}
int PathQuery(int u,int v){ //路径查询
    int ans = 0;
    while(top[u] != top[v]){
        if(dep[top[u]] > dep[top[v]]) swap(u,v);
        ans += sgt.query(1,n,1,pos[top[v]],pos[v]); //累加
        ans %= R;
        v = prv[top[v]]; //往上跳
    }
    ans += sgt.query(1,n,1,min(pos[u],pos[v]),max(pos[u],pos[v]));
    return ans%R;
}
int SubTreeQuery(int x){ //子树查询
    return sgt.query(1,n,1,pos[x],pos[x]+sz[x]-1); //直接返回
}

三 图论应用

树链剖分是一种针对树上问题的很优秀的处理想法。正是因为它太优秀了，所以他并不仅仅能当一个数据结构用，甚至可以被用来解决图论问题。

准确的说，树链剖分就是一种把“树”映射成“链”的想法，就像上面所描述的那样。对于这个“链”，我们就能进行很多处理，诸如挂上线段树，维护前缀和之类。通过这些优秀的数据结构，我们就可以很好的解决有关树上路径的诸多问题。

1 点对LCA

最近公共祖先（Least Common Ancestors，LCA）也是可以用LCA求的。我们对树上的一个点对$(u,v)$进行跳链操作，直到两点处于一条重链上停止，那么此时$u,v$中深度浅（更靠近根）的那个就是$(u,v)$的LCA。

实际上这样就不需要再在树剖上挂线段树了。于是代码长这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
const int CN = 5e5+5;

class fs{ //边表
  public: int to,nxt;
    void init(int t,int n) {to=t;nxt=n;}
}E[CN<<1];
int hd[CN],ecnt = 0;
void add(int x,int y){
    E[++ecnt].init(y,hd[x]);
    hd[x] = ecnt;
}

/*SGT*/
int dep[CN],prv[CN],imp[CN],sz[CN],top[CN];
void init1(int u){
    dep[u] = dep[prv[u]]+1;
    sz[u] = 1;
    int mx = 0;
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(!dep[v]){
            prv[v] = u;
            init1(v);
            sz[u] += sz[v];
            if(sz[v] > mx) mx = sz[imp[u] = v];
        }
    }
}
void init2(int u,int t){
    top[u] = t;
    if(!imp[u]) return;
    init2(imp[u], t);
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(v!=prv[u] && v!=imp[u]) init2(v, v);
    }
}
int LCA(int u,int v){ //查询 (u,v) 的LCA
    while(top[u] != top[v]){ //跳链
        if(dep[top[u]] > dep[top[v]]) swap(u,v);
        v = prv[top[v]];
    }
    if(dep[u] > dep[v]) swap(u,v); //让 u 成为深度浅的那个
    return u;
}

一个LCA的例题：HDU 4547 CD Opt。

2 点对路径和

「HDU 2874」Connections between cities

给你多棵树，树有边权。每次询问一个点对$(u,v)$间的路径上的边权和，若不连通输出 Not connected。

首先是判联通，这个可以用并查集，不多讲了。

前面提到过树剖在处理边权问题的时候，可以把边权改点权。具体的做法是让边$u\to v$的权变成$v$点的权，因为一个儿子节点只对应一个父节点，也就是只对应一条通向父节点的边。

但是这样实际在统计边权的时候上会多统计一条边，也就是两个点的LCA对应的那条边。于是我们在两个点跳到同一条重链之后（也就是求出了LCA），要把LCA往它的重儿子偏移一个节点，然后再统计边权和。但是有时候还会使得最后这个区间不存在，那么我们加个特判就好了。

另一个边权问题的例子：USACO11DEC Grass Planting。

于是点对间的边权和问题就被转化成了点对间的点权和问题。并且这个点权和还不需要支持修改，于是我们只需要树剖之后，维护一个前缀和就好了。

代码长这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
const int CN = 1e4+4;
const string FAIL = "Not connected";

class fs{ //边表
  public: int from,to,nxt,dist;
    void init(int f,int t,int n,int d)
    {from = f; to = t; nxt = n; dist = d;}
}E[CN<<1];
int hd[CN],ecnt = 0;
void add(int x,int y,int z){
    E[++ecnt].init(x,y,hd[x],z);
    hd[x] = ecnt;
}
void fs_init(){memset(hd,0,sizeof(hd)); ecnt = 0;} //边表初始化（多组数据！）

class ufs{ //并查集，用来判联通
  public: int fa[CN];
    ufs() {for(int i=0;i<=10001;i++) fa[i] = i;}       //构造函数
    void init() {for(int i=0;i<=10001;i++) fa[i] = i;} //初始化
    int find(int x) {return fa[x] == x ? x : fa[x] = find(fa[x]);}
    void merge(int x,int y) {fa[find(x)] = find(y);}
    bool exm(int x,int y) {return find(x) != find(y);}
}con;

int n; //点数

/*SGT*/
int top[CN],pos[CN],sz[CN],imp[CN],prv[CN],dep[CN],idx;
void sgt_init(){ //树剖初始化
    memset(top,0,sizeof(top)); memset(pos,0,sizeof(pos));
    memset(sz,0,sizeof(sz)); memset(imp,0,sizeof(imp));
    memset(prv,0,sizeof(prv)); memset(dep,0,sizeof(dep));
    idx = 0;
}
void init1(int u){
    dep[u] = dep[prv[u]]+1;
    sz[u] = 1;
    int mx = 0;
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(v != prv[u]){
            prv[v] = u;
            init1(v);
            sz[u] += sz[v];
            if(sz[v] > mx) mx = sz[imp[u] = v];
        }
    }
}
void init2(int u,int t){
    pos[u] = ++idx;
    top[u] = t;
    if(!imp[u]) return;
    init2(imp[u],t);
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(v!=prv[u] && v!=imp[u]) init2(v,v);
    }
}
int sum[CN]; //前缀和
void NodeValInit(int u){ //边权转点权
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(v != prv[u]){
            sum[pos[v]] = E[k].dist;
            NodeValInit(v);
        }
    }
}
void SGT_Prep(){ //初始化树剖的主调用函数
    sgt_init(); 
    for(int i=1;i<=n;i++) //枚举根，因为可能有多棵树
        if(!dep[i]){
            init1(i); init2(i,i); NodeValInit(i);
        }
    for(int i=1;i<=n;i++) sum[i] += sum[i-1]; //推前缀和
}
int PathQuery(int u,int v){ //回答路径查询
    int rec = 0;
    while(top[u] != top[v]){
        if(dep[top[u]] > dep[top[v]]) swap(u,v);
        rec +=  sum[pos[v]]-sum[pos[top[v]]-1];
        v = prv[top[v]];
    }
    if(dep[u] > dep[v]) swap(u,v); //u is lca
    u = imp[u]; //下移一个节点
    if(dep[u] > dep[v]) return rec; //区间不存在
    return rec + sum[pos[v]]-sum[pos[u]-1];
}

3 重构树后的树链剖分

「NOIP2013 D1T3」货车运输

给定一张不保证是树的图，边有边权。定义一条$x\to y$的路径的宽度是这条路径上所有边权的最小值。每次询问图上两点对$(u,v)$间的所有路径上，宽度最大的那条路径的宽度值。

两个相邻的点间可能有多条边，那么肯定要保留边权大的。推广，考虑到要保证图的连通性，我们需要选出最少的边，使每条边的权值都尽量大，并且要求这些边不能使图的连通性改变。

那么也就是最大生成树了。重构最大生成树之后，剩下的问题就是一个查询两点路径上的最小边权。这个可以树剖，然后挂一个线段树就好了。

还有一个细节：图不保证联通。这个像上面一样用并查集维护就好了。

代码长这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
const int CN = 1e5+4;
const int INF = 0x3f3f3f3f;

class fs{ //边表
  public: int from,to,nxt,dist;
    void init(int f,int t,int n,int d) {from=f;to=t;nxt=n;dist=d;}
    bool operator < (const fs &a)const {return dist > a.dist;} //最大生成树
}E[CN<<1];
int hd[CN],ecnt = 0;
void add(int x,int y,int z){
    E[++ecnt].init(x,y,hd[x],z);
    hd[x] = ecnt;
}
void fs_init() {memset(hd,0,sizeof(hd)); ecnt = 0;} //边表初始化

class ufs{ //并查集
  public: int fa[CN];
    ufs() {for(int i=0;i<=10001;i++) fa[i]=i;}
    void init() {for(int i=0;i<=10001;i++) fa[i]=i;} //初始化，为了循环利用空间
    int find(int x) {return fa[x]==x? x : fa[x]=find(fa[x]);}
    void merge(int x,int y) {fa[find(x)] = find(y);}
    bool exm(int x,int y) {return find(x) != find(y);}
}con;

int n; //点数

/*MST*/
int X[CN],Y[CN],Z[CN]; //记录选中的边
void MST(){ //最大生成树 Kruskal
    sort(E+1,E+ecnt+1);
    for(int k=1;k<=ecnt;k++){
        int x = E[k].from,y = E[k].to;
        if(!con.exm(x,y)) continue;
        con.merge(x,y); ++X[0];
        X[X[0]] = x; Y[X[0]] = y; Z[X[0]] = E[k].dist;
    }
}
void ReBuild(){ //重构树
    fs_init(); con.init(); //初始化图
    for(int i=1;i<n;i++){
        add(X[i],Y[i],Z[i]),add(Y[i],X[i],Z[i]);
        if(con.exm(X[i],Y[i])) con.merge(X[i],Y[i]); //维护联通性
    }
}
/*MST end*/

/*SGT*/
class SGT{ //线段树 支持查询静态区间最小值
  public: int d[CN<<1],org[CN];
    void build(int l,int r,int k){
        if(l == r) return (void)(d[k] = org[l]);
        int m = (l+r)>>1;
        build(l,m,k<<1); build(m+1,r,k<<1|1);
        d[k] = min(d[k<<1], d[k<<1|1]);
    }
    int query(int l,int r,int k,int s,int t){
        if(s<=l && r<=t) return d[k];
        int m = (l+r)>>1,rec = INF;
        if(s <= m) rec = min(rec, query(l,m,k<<1,s,t));
        if(m < t) rec = min(rec, query(m+1,r,k<<1|1,s,t));
        return rec;
    }
}sgt;
int dep[CN],pos[CN],sz[CN],top[CN],prv[CN],imp[CN],idx = 0;
void init1(int u){
    dep[u] = dep[prv[u]]+1;
    sz[u] = 1;
    int mx = 0;
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(!dep[v]){
            prv[v] = u;
            init1(v);
            sz[u] += sz[v];
            if(sz[v] > mx) mx = sz[imp[u] = v];
        }
    }
}
void init2(int u,int t){
    pos[u] = ++idx;
    top[u] = t;
    if(!imp[u]) return;
    init2(imp[u], t);
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(v!=prv[u] && v!=imp[u]) init2(v, v);
    }
}
void NodeValInit(int u){ //边权转点权
    for(int k=hd[u];k;k=E[k].nxt){
        int v = E[k].to;
        if(v != prv[u]){
            sgt.org[pos[v]] = E[k].dist;
            NodeValInit(v);
        }
    }
}
void SGT_Prep(){ //初始化树剖的主调用函数
    for(int i=1;i<=n;i++){ //枚举根
        if(dep[i]) continue;
        init1(i); init2(i, i); NodeValInit(i);
    }
    sgt.build(1,n,1); //初始化线段树
}
int PathQuery(int u,int v){ //求 (u,v) 路径上的最小值
    int mn = INF;
    while(top[u] != top[v]){
        if(dep[top[u]] > dep[top[v]]) swap(u,v);
        mn = min(mn, sgt.query(1,n,1, pos[top[v]],pos[v]));
        v = prv[top[v]];
    }
    if(dep[u] > dep[v]) swap(u,v); //u is LCA
    u = imp[u]; //下移一个节点
    if(dep[u] > dep[v]) return mn;
    return min(mn, sgt.query(1,n,1, pos[u],pos[v]));
}
/*SGT end*/

int main()
{
    ... //Scan Data
    
    /*重构树*/
    MST(); ReBuild();
    
    /*初始化树剖*/
    SGT_Prep();
    ... //Answer Question
    
    return 0;
}

树链剖分

https://big-news.cn/2019/07/18/树链剖分/

作者

ce-amtic

发布于

2019-07-18

更新于

2023-04-15

许可协议

CC BY-NC-SA 4.0

#

评论

目录

推荐阅读

Your browser is out-of-date!

Update your browser to view this website correctly.&npsb;Update my browser now

×

×