「题解」天际线

Latium省的Genoa是亚平宁半岛西海岸北端的一片土地，自然资源丰富，却无人居住。你受到罗马执政官Caesar的委任，前往Genoa建立新的城市…..

一 题目

原题链接

描述

Latium省的Genoa是亚平宁半岛西海岸北端的一片土地，自然资源丰富，却无人居住。你受到罗马执政官Caesar的委任，前往Genoa建立新的城市。Caesar对这次任务的要求是在Genoa这片土地上建立起一座繁荣的城市，他将以此作为衡量你的表现的标准。

正在你大刀阔斧地进行城市建设的时候，Caesar突然写信给你，说他要检查Genoa的建设情况。Caesar希望知道你的城市是什么样子，但是他又非常的忙，所以他只要你描述一下城市的轮廓就可以了，他将依照城市的轮廓决定你的薪水。

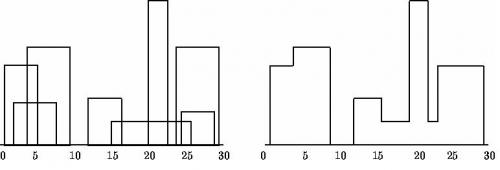
怎样描述一个城市的轮廓呢？我们知道Genoa所有的建筑共享一个地面，你可以认为它是水平的。所有的建筑用一个三元组（Li,Hi,Ri）其中Li和Ri分别是建筑的左坐标和右坐标，Hi就是建筑的高度。在下方所示的图表中左边建筑物描述如下(1,11,5),(2,6,7),(3,13,9),(12,7,16),(14,3,25),(19,18,22),(23,13,29),(24,4,28)，右边用轮廓线的顺序（1,11,3,13,9,0,12,7,16,3,19,18,22,3,23,13,29,0）表示：

输入

在输入数据中，你将得到一系列表示建筑的三元组。在输入数据中所有建筑的坐标中的数值都是小于10000的正整数，且至少有1幢建筑，最多有5,000幢建筑。在输入输入中每幢建筑的三元组各占一行。三元组中的所有整数应由一个或多个空格分开。

输出

在输出数据中，你被要求给出城市的轮廓线。你可以这样来描述：对于所有轮廓线上的折点，按顺序排好，第奇数个点输出x坐标，第偶数个点输出y坐标，两个数之间用空格分开。

---

二 题解

扫描线+线段覆盖水题，不懂请参见「题解」Atlantis。

于是乎说一下我的AC过程吧。
40min打完代码并调好样例，第一次提交拿了80pts，然后测试数据不给，只好自己去写对拍。
然后我就可以顺理成章的贴出对拍的模板：

run.bat

@echo off  
:loop  
    g.exe>data.in  
    std.exe<data.in>std.out
    db.exe<data.in>my.out  
    fc my.out std.out  
if not errorlevel 1 goto loop  
pause  
goto loop

顺便再贴一下上面这种样式的代码块的插入代码（对，这就是水博客）。

{% codeblock [title] [lang:language] [url] [link text] %}
code snippet
{% endcodeblock %}

既然对拍的板子贴出来了，那么我水博客的目的达成了，然后发现应该一次性把在同一横坐标上的所有线段处理完，然后就AC了。

顺便一说，这代码反手就被我hack掉了。有什么办法么，我都AC了……

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;

const int CN = 4e6+6;

int read(){
    int s=0,ne=1; char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') ne=-1;
    for(;c>='0'&&c<='9';c=getchar()) s=(s<<1)+(s<<3)+c-'0';
    return s*ne;
}

int n;

class locat{
  public: int x,y;
    bool operator < (const locat &a)const{
        if(x == a.x) return y < a.y;
        return x < a.x;
    }
}ans[CN]; 
int acnt = 0;

//Segment Cover 
class Segment{
  public: int r,x,k;
    bool operator < (const Segment &a)const
    {return x < a.x;}
}seg[CN];
int scnt = 0;

int pos[CN],pcnt;
class node{
  public: int len,cnt;
};
class SGT{
  public:
      node d[CN<<2];
      int GetLen(int l,int r,int k){
          if(d[k].cnt) return pos[r+1]-pos[l];
          if(l == r) return 0;
          return d[k<<1].len + d[k<<1|1].len;
    }
      void modify(int l,int r,int k,int s,int t,int x){
          if(s<=l && r<=t){
              d[k].cnt += x;
              d[k].len = GetLen(l,r,k);
              return;
        }
        int m = (l+r)>>1;
        if(s <= m) modify(l,m,k<<1,s,t,x);
        if(m < t) modify(m+1,r,k<<1|1,s,t,x);
        d[k].len = GetLen(l,r,k);
    }
}sgt;

void SegmentCover(int i){
    int l = 1;
    int r = lower_bound(pos+1,pos+pcnt+1,seg[i].r)-pos-1;
    sgt.modify(1,pcnt,1,l,r,seg[i].k);
}

int main()
{
    //freopen("data.in","r",stdin);
    
    n = 0;
    int x,y,z;
    while(~scanf("%d%d%d",&x,&y,&z)){
        n++;
        seg[scnt+1].r = y; seg[scnt+1].x = x; seg[scnt+1].k = 1;
        seg[scnt+2].r = y; seg[scnt+2].x = z; seg[scnt+2].k = -1;
        scnt += 2;
        pos[n] = y;
    }
    pos[++n] = 0; //防止出锅 
    
    //离散化 
    sort(seg+1,seg+scnt+1);
    sort(pos+1,pos+n+1);
    pcnt =1;
    for(int i=2;i<=n;i++) 
        if(pos[i] != pos[i-1])
            pos[++pcnt] = pos[i];
    //solve
    int prvh = 0;
    for(int i=1;i<=scnt;i++){
        while(seg[i].x==seg[i+1].x && i<scnt) 
            SegmentCover(i),i++;
        SegmentCover(i);
        if(sgt.d[1].len != prvh){
            ans[++acnt].x = seg[i].x;
            ans[acnt].y = prvh;
            prvh = sgt.d[1].len;
            ans[++acnt].x = seg[i].x;
            ans[acnt].y = prvh;
        }
    }
    
    //print
    for(int i=1;i<=acnt;i++)
        if(i & 1) printf("%d ",ans[i].x);
            else printf("%d ",ans[i].y);
    
    return 0;
}